Valid BST

Problem

First Try

  • a tree can be traversed in three different ways
  • in this case we try to use pre-order traversal since a tree can be determined as BST based on the BST-ness of its child sub-trees
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
bool isValidBST(TreeNode* root) {

    // edge case
    if (root == nullptr) return true;

    // base case of leaves
    if (!root->left && !root->right) return true;

    bool left_valid = true; // assume true...maybe no left subtree
    bool right_valid= true; // assume true...maybe no right subtree
    if (root->left) {
        if (root->left->val < root->val) left_valid = isValidBST(root->left);
        else return false;
    }
    if (root->right) {
        if (root->right->val > root->val) right_valid = isValidBST(root->right);
        else return false;
    }

    return (left_valid && right_valid);
}

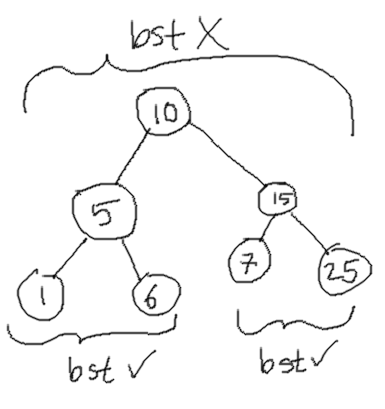
The problem with the above solutions is that it doesn’t work for cases like the following where a number smaller than root appears on the right even though the sub-tree is a valid BST.

Alternative Approach

Since the approach above is incomplete, let’s think of what a proper BST looks like.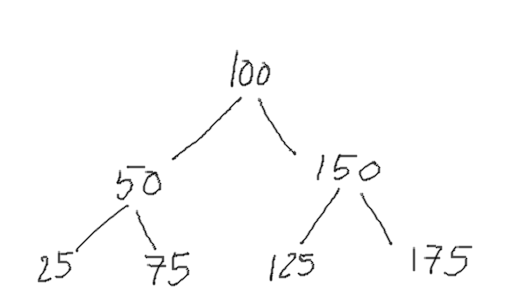

If we perform an inorder traversal of this we see that the numbers are all in ascending order.

1
25,50,75,100,125,150,175

So…we can do an inorder traversal and ensure that at any point when we visit a node the last node we visited has the smaller value!

Final solution

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    bool isValidBST(TreeNode* root) {
    stack<TreeNode*> s;
    int prev_val = 0;
    TreeNode *farLeft = nullptr;

    // keep a track of the pointer so we know during travesal
    // that we are testing the left most node

    while (!s.empty() || root != nullptr) {
        if (root != nullptr) {
            s.push(root);
            root = root->left;
        } else {
            root = s.top();
            s.pop();
            if (!farLeft) {
                farLeft = root;
            } else {
                if (root->val <= prev_val) return false;
            }
            prev_val = root->val;
            root = root->right;
        }

    }
    return true;
}

};

It’s important to keep a track of the pointer since we need to know when the left most node is hit. If we pre-populate with min value such as int prev_val = MIN_INT; then that will not work in some cases when MIN_INT is actually a value of the tree. Can you see how?

Tree traversals can be done both using recursive and iterative approaches. Recursive solutions may be more intuitive but they suffer from the possibility of stack overflow. I will plan to have a separate post comparing each of the traversals using both approaches.