Traversing N-ary trees

Post Order

Problem

First iteration

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
/*
// Definition for a Node.
class Node {
public:
    int val;
    vector<Node*> children;

    Node() {}

    Node(int _val, vector<Node*> _children) {
        val = _val;
        children = _children;
    }
};
*/
class Solution {
public:
    vector<int> postorder(Node* root) {
        stack<int> s;
        vector<int> v;
        if (root == nullptr) return v;
        s.push(root);
        while(!s.empty()) {
            Node *node = s.top();
            s.pop();
            v.insert(v.begin(), node->val);
            for (Node* c: node->children) {
                s.push(c);
            }
        }
        return v;
    }
};

Recursive

Preorder

todo

Inorder

todo

basic-calc

Problem

Analysis

  • we need to skip spaces
  • we can use a recursive function since each expression is a subproblem
1
2
3
4
4-3+6-(45+6-(77 - 5) + 3) is equivalent to
4-3+6-45-6+77-5+3
      ^---------- negative
          ^------- positive since two negatives

So we can keep track of the sign changes

Attempt

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50

class Solution {
    /*
     Contains -1's
     */
    int getsign(vector<int>& v) {
        int sign = 1;
        for (int e: v) {
            sign *= e;
        }
        return sign;
    }
    int getnum(string s, int& i) {
        string n;
        while (i < s.size() && isdigit(s[i])) {
            n+=s[i];
            i++;
        }
        return stoi(n);
    }
public:
    int calculate(string s) {
        vector<int> signs;
        for (int i = 0; i < s.size(); i++) {
            if (isdigit(s[i])) {
                num = getnum(s, i)
                sum += sign * num;
            } else if (s[i] == '(') {
                // when we start a new group
                // we calculate the new sign to
                // apply
                // first push the last sign we e
                signs.push_back(sign);
                sign = getsign(signs);

                // skip over any extra '('?
                //while (i < s.size() && s[i] == '(') i++;

            } else if (s[i] == ')') {
                // we need to pop the signs stack
                signs.pop_back();
                // todo skip over extra ')'?
            } else if (s[i] == '-') {
                sign = -1;
            } else if (s[i] == '+') {
                sign = 1;
            }
        }
    }
};

ATtempt 2

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56


class Solution {
    /*
     Contains -1's
     */
    int getsign(vector<int>& v) {
        int sign = 1;
        for (int e: v) {
            sign *= e;
        }
        return sign;
    }
    int getnum(string s, int& i) {
        string n;
        while (i < s.size() && isdigit(s[i])) {
            n+=s[i];
            i++;
        }
        return stoi(n);
    }
public:
    int calculate(string s) {
        vector<int> signs = {1};
        int sum = 0;
        int num = 0;
        int sign = 1;
        for (int i = 0; i < s.size(); i++) {
            if (isdigit(s[i])) {
                num = getnum(s, i);
                sum += sign * num;
                cout << "d = " << sign * num << endl;
            } else if (s[i] == '(') {
                // when we start a new group
                // we calculate the new sign to
                // apply
                // first push the last sign we e
                signs.push_back(sign);
                //sign = getsign(signs);

                // skip over any extra '('?
                //while (i < s.size() && s[i] == '(') i++;

            } else if (s[i] == ')') {
                // we need to pop the signs stack
                signs.pop_back();
                // todo skip over extra ')'?
            } else if (s[i] == '-') {
                sign = signs.back() * -1;
            } else if (s[i] == '+') {
                sign = signs.back();
            }
        }
        return sum;
    }
};

Note about performance

TODO

remove-linked-list-elem

Problem

Analysis

  • with linked lists, if we are removing something we may need to update head
  • value can occur multiple times so we need to remove both
  • traversing linked list takes O(n)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode(int x) : val(x), next(NULL) {}
 * };
 */
class Solution {
public:
    ListNode* removeElements(ListNode* head, int val) {
        if (head == nullptr) return head;
        ListNode *p = head;

        // handle val(s) at head
        while (p && (p->val == val)) {
            ListNode *t = p;
            p = p->next;
            delete t;
        }
        // we need to update the head
        // if we deleted any nodes above
        head = p;

        // if no more nodes just return
        if !(head) return head;

        // handle the rest of the list
        while (p->next) {
            if (p->next->val == val) {
                ListNode* t = p->next;
                p->next = p->next->next;
                delete t;
            }
        }

        return head;
    }
};

Next Attempt

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode(int x) : val(x), next(NULL) {}
 * };
 */
class Solution {
public:
    ListNode* removeElements(ListNode* head, int val) {
        if (head == nullptr) return head;
        ListNode *p = head;

        // handle val(s) at head
        while (p && (p->val == val)) {
            ListNode *t = p;
            p = p->next;
            delete t;
        }
        // we need to update the head
        // if we deleted any nodes above
        head = p;

        // if no more nodes just return
        if (!head) return head;

        // handle the rest of the list
        while (p && p->next) {
            if (p->next->val == val) {
                ListNode* t = p->next;
                p->next = p->next->next; // point to the node after next
                delete t; // delete the next one
            }
            p = p->next; // move to next node
        }

        return head;
    }
};

Almost Final Solution

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode(int x) : val(x), next(NULL) {}
 * };
 */
class Solution {
public:
    ListNode* removeElements(ListNode* head, int val) {
        if (head == nullptr) return head;
        ListNode *p = head;

        // handle val(s) at head
        while (p && (p->val == val)) {
            ListNode *t = p;
            p = p->next;
            delete t;
        }
        // we need to update the head
        // if we deleted any nodes above
        head = p;

        // if no more nodes just return
        if (!head) return head;

        // handle the rest of the list
        ListNode *prev = p;
        ListNode *cur = p->next;
        while (cur) {
            ListNode* t = nullptr;
            if (cur->val == val)) {
                t = cur;
                prev->next = cur->next; // point to the node after next
            }
            cur = cur->next; // move to next node
            if (t) delete t;
        }

        return head;
    }
};

Final Solution

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
class Solution {
public:
    ListNode* removeElements(ListNode* head, int val) {
        if (head == nullptr) return head;
        ListNode *p = head;

        // handle val(s) at head
        while (p && (p->val == val)) {
            ListNode *t = p;
            p = p->next;
            delete t;
        }
        // we need to update the head
        // if we deleted any nodes above
        head = p;

        // if no more nodes just return
        if (!head) return head;

        // handle the rest of the list
        ListNode *prev = p;
        ListNode *cur = p->next;
        while (cur) {
            //if (cur) { cout << cur->val << endl; }
            ListNode* t = nullptr;
            if (cur->val == val) {
                t = cur;
                prev->next = cur->next; // point to the node after next
            } else {
                // prev is only updated if we don't delete a node
                prev = cur;
            }
            cur = cur->next; // always move to next node

            if (t) delete t;
        }

        return head;
    }
};

Amended Solution

While the above solution is functional, it’s pretty long. We can remove the need for the special case of the val being at the head by using some pointer magic.

TODO: add picture

1
2
3
4
5
6
7
8
9
10
11
12
13
14
class Solution {
public:
    ListNode* removeElements(ListNode* head, int val) {
		ListNode **cur = &head;
		while(*cur != NULL)
		{
			if((*cur)->val == val)
				*cur = (*cur)->next;
			else
				cur = &((*cur)->next);
		}
		return head;
    }
};

Range Sum Query Immutable

Problem

Analysis

  • We need to set the lower and upper bounds as per given indices.
    Example:

    1
    2
    3
    4
    5
    for given example
    sumRegion(2, 1, 4, 3)

    we iterate row from 2 to 4 inclusive
    we iterate col from 1 to 3 inclusive

  • matrix is immutable

First Attempt

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
class NumMatrix {
    int r1, r2;
    int c1, c2;
    int rsize, csize;
    vector<vector<int>> m;
public:
    NumMatrix(vector<vector<int>> matrix) {
        rsize = matrix.size();
        csize = matrix[0].size();
        for (auto e: matrix) {
            m.push_back(e);
        }
    }

    int sumRegion(int row1, int col1, int row2, int col2) {
        if !((0 <= row1 < rsize) &&
             (0 <= row2 < rsize) &&
             (0 <= col1 < csize) &&
             (0 <= col2 < csize)
            )
            return 0;
        int sum = 0;
        for (int r = row1; r <= row2; r++) {
            for (int c = col1; c <= col2; c++) {
                sum += m[r][c];
            }
        }


    }
};

/**
 * Your NumMatrix object will be instantiated and called as such:
 * NumMatrix obj = new NumMatrix(matrix);
 * int param_1 = obj.sumRegion(row1,col1,row2,col2);
 */

Amended Solution

While the solution above is in the right spirit. The execution suffers.

  1. The expressions of the form (0 <= row1 < rsize) are erroneous.
  2. We should check for the case of empty matrix
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
class NumMatrix {
    int r1 = 0, r2 = 0;
    int c1 = 0, c2 = 0;
    int rsize = 0, csize = 0;
    vector<vector<int>> m;
public:
    NumMatrix(vector<vector<int>> matrix) {
        if (!matrix.empty()) {
            rsize = matrix.size();
            csize = matrix[0].size();
            for (auto e: matrix) {
                m.push_back(e);
            }
        }
    }

    int sumRegion(int row1, int col1, int row2, int col2) {
            if (row1 < 0 || row1 > rsize ||
               row2 < 0 || row2 > rsize ||
               col1 < 0 || col1 > csize ||
               col2 < 0 || col2 > csize)
            {
             return -1;
            }
        int sum = 0;
        for (int r = row1; r <= row2; r++) {
            for (int c = col1; c <= col2; c++) {
                sum += m[r][c];
            }
        }

        return sum;
    }
};

/**
 * Your NumMatrix object will be instantiated and called as such:
 * NumMatrix obj = new NumMatrix(matrix);
 * int param_1 = obj.sumRegion(row1,col1,row2,col2);
 */

decode-str

https://leetcode.com/problems/decode-string/description/

Notes

  • strings within strings would also need to be decoded
  • the function that generates the string could be recursive since each sub-problem resembles the original problem
  • number will be positive int
  • no spaces
  • matching brackets guaranteed

    Examples

    1
    2
    3
    4
    Input:

    "abcd10[a6[zd]]"
    "14[w]100[dfg9[ik]]"

It’s really important to try several types of examples out before we jump into the final solution. One important point to note is that we need to keep passing in pos as a reference it needs to be shared across all function invocations since we are moving through the string in one pass and need to keep track of the number of characters consumed. The solution below is a step in the right direction but has some flaws as noted below.

First Try

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
class Solution {
    int pos = 0;
    /*
    Parsing starts when we encounter a number
    number can be multiple digits
    We stop parsing and return generated string
    when we encounter matching `]`
    */
    string parse(string s, int& pos, int len) {
        string res;
        string rep;
        for (; pos < s.size(); pos++) {
            if (isdigit(s[pos]) {
                rep += s[pos];
            } else if (isalpha(s[pos]) {
                res += s[pos];
            // need to explicitly update position?
            } else if (s[pos++] == ']')
            {
                for (int j = 2; j <= len; j++) {
                    res += res;
                }
            } else if (s[pos++] == '[')
            {

                res += parse(s, pos, stoi(rep));
            }

        }

        return res;
    }
public:
    string decodeString(string s) {

        // if string starts with number
        // we need to compute the number
        if (isdigit(s[0])) {
            string len;
            int i = 0;
            for (; i < s.size(); i++) {
                if (s[i] == '[') {
                    len = s.substr(0,i);
                    i++;
                    break;
                }
            }
            return parse(s, i, stoi(len));

        }
        // else just use 1
        else {
            return parse(s, pos, 1);
        }

    }
};

Issues

  1. decodeString() doesn’t need that ugly logic. We can just call parse().
  2. if (s[pos++] == ']' is incorrect here since it will increment position and then check the value, which is hardly what we want.

Accepted Solution

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
class Solution {
    int pos = 0;
    /*
    Parsing starts when we encounter a number
    number can be multiple digits
    We stop parsing and return generated string
    when we encounter matching `]`
    */
    string parse(string s, int& pos, int len) {
        string res;
        string rep = "";
        cout <<  " at pos = " << pos << " length = " << len << endl;
        for (; pos < s.size(); pos++) {
            if (isdigit(s[pos])) {
                rep += s[pos];

            } else if (isalpha(s[pos])) {
                res += s[pos];
            // need to explicitly update position?
            } else if (s[pos] == ']')
            {
                string tmp = res;
                for (int j = 2; j <= len; j++) {
                    res += tmp;
                }
                /*
                    we need to return here since each function
                    call only deals with [...] pair.
                    any other [...] pairs within are handled
                    by a seperate invocation of this function
                */
                break;

            } else if (s[pos] == '[')
            {

                pos++;
                res += parse(s, pos, (rep != "")?stoi(rep):1);
                // need to reset rep since we may have many
                // groups
                // ex: abc[eegh]lki55[tt]
                 rep = "";

            }
            cout << "res = " << res << " rep = " << rep << endl;

        }
        cout << "ret = " << res << endl;
        return res;
    }
public:
    string decodeString(string s) {

       return parse(s, pos, 1);


    }
};

Valid BST

Problem

First Try

  • a tree can be traversed in three different ways
  • in this case we try to use pre-order traversal since a tree can be determined as BST based on the BST-ness of its child sub-trees
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
bool isValidBST(TreeNode* root) {

    // edge case
    if (root == nullptr) return true;

    // base case of leaves
    if (!root->left && !root->right) return true;

    bool left_valid = true; // assume true...maybe no left subtree
    bool right_valid= true; // assume true...maybe no right subtree
    if (root->left) {
        if (root->left->val < root->val) left_valid = isValidBST(root->left);
        else return false;
    }
    if (root->right) {
        if (root->right->val > root->val) right_valid = isValidBST(root->right);
        else return false;
    }

    return (left_valid && right_valid);
}

The problem with the above solutions is that it doesn’t work for cases like the following where a number smaller than root appears on the right even though the sub-tree is a valid BST.

Alternative Approach

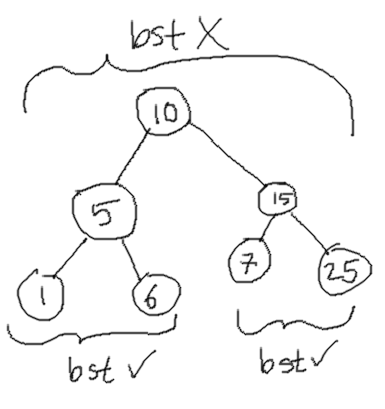
Since the approach above is incomplete, let’s think of what a proper BST looks like.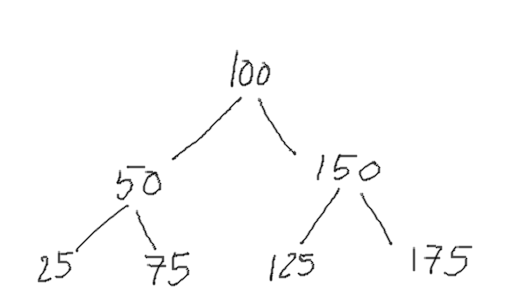

If we perform an inorder traversal of this we see that the numbers are all in ascending order.

1
25,50,75,100,125,150,175

So…we can do an inorder traversal and ensure that at any point when we visit a node the last node we visited has the smaller value!

Final solution

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    bool isValidBST(TreeNode* root) {
    stack<TreeNode*> s;
    int prev_val = 0;
    TreeNode *farLeft = nullptr;

    // keep a track of the pointer so we know during travesal
    // that we are testing the left most node

    while (!s.empty() || root != nullptr) {
        if (root != nullptr) {
            s.push(root);
            root = root->left;
        } else {
            root = s.top();
            s.pop();
            if (!farLeft) {
                farLeft = root;
            } else {
                if (root->val <= prev_val) return false;
            }
            prev_val = root->val;
            root = root->right;
        }

    }
    return true;
}

};

It’s important to keep a track of the pointer since we need to know when the left most node is hit. If we pre-populate with min value such as int prev_val = MIN_INT; then that will not work in some cases when MIN_INT is actually a value of the tree. Can you see how?

Tree traversals can be done both using recursive and iterative approaches. Recursive solutions may be more intuitive but they suffer from the possibility of stack overflow. I will plan to have a separate post comparing each of the traversals using both approaches.

Genetic Mutations

Problem

First Try

  • Recursive DFS?
    Let’s see some examples.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31

start: "AAAAACCC"
end:   "AACCCCCC"
bank: ["AAAACCCC", "AAACCCCC", "AACCCCCC"]

return: 3

we need to check from start of string which letter we can change so that string exists in bank

start: "AA[A][A][A]CCC"
end:   "AA[C][C][C]CCC"

tmp string AA(C)AACCC in bank? no
AAA(C)ACCC in bank? no
AAAA(C)CCC ? yes!
update string to AAAACCCC

start: AAAACCCC
end: AACCCCCC

check if in bank:
AA(C)ACCCC? no
AAA(C)CCCC? yes!

start:AAACCCCC
end:AACCCCCC

check if in bank:
AA(C)CCCCC? yes!

done....3 tries

Attempted Solution

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
int dfs(string start, string end, vector<string>& bank, int tries) {
    //base case

    if (start == end) return tries;

    for (int i = 0; i < start.size(); i++) {


        if (start[i] == end[i]) continue; // nothing to do if letter is same
        // if letter is different in end string then we copy that letter and
        // check if it exists in bank
        string tmp = start;
        tmp[i] = end[i];
        int ret = -1;
        if (find(bank.begin(), bank.end(), tmp) != bank.end()) {
            ret = dfs(tmp, end, bank, tries+1);
        }
        if (ret != -1) return ret;
    }

    return -1; //oops don't forget this...if not found at all
}
int minMutation(string start, string end, vector<string>& bank) {
    return dfs(start, end, bank, 0);
}

Unfortunately, there is a major flaw in the logic above. The problem is that we are only flipping the letters as per the end string. This worked in the example I chose above, but there may be paths we have not considered. This means we may not always find the path to the end string.

We should flip letters to {A, C, T, G} and not just the ones we want to change for the end string.

Notes for next approach

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
keep a visited vector of booleans to denote when we have visited a particular string from the bank

Using this example
start: "AACCGGTT"
end: "AAACGGTA"
["AACCGATT","AACCGATA","AAACGATA","AAACGGTA"]

Given:
queue Q of visiting
set V of visited
set B of Bank of valid strings
List L of available letters
level = 0
string target

Q.add(start)
while !Q.empty
    s = Q.pop()
    level++
    if s == target return level
    V.push(s)
    for i=0 -> s.size()
        for letter l2 in L
            char c = s[i]
            s[i] = l2
            if (s in B) and (s not in V)
                Q.push(s)
            end
            s[i] = c // restore char?
        end
    end
end
return -1

Buggy solution below

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
int minMutation(string start, string end, vector<string>& bank) {
    unordered_set<string> V; // visited
    unordered_set<string> B; // bank
    vector<string> Q; // work queue
    vector<char> letters = {'A', 'C', 'G', 'T'};
    // copy strings from bank to set for quicker lookup
    for (auto e: bank) {
        B.push_back(e);
    }

    Q.push_back(start);

    while (!Q.empty()) {
        string s = Q.front();
        Q.erase(Q.begin());
        level++;
        if (s == end) return level;
        for (int i = 0; i < s.size(); i++) {
            char c = s[i];
            for (auto l: letters) {
                s[i] = l;
                if (!V.find(s) && B.find(s)) {
                    Q.push_back(s);
                }
                s[i] = c;
            }
        }
    }

    return -1;
}

FIxed

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
class Solution {
public:
    int minMutation(string start, string end, vector<string>& bank) {
    unordered_set<string> V; // visited
    unordered_set<string> B; // bank
    vector<string> Q; // work queue
    vector<char> letters = {'A', 'C', 'G', 'T'};
    int level = 0;
    // copy strings from bank to set for quicker lookup
    for (auto e: bank) {
        B.insert(e);
    }

    Q.push_back(start);

    while (!(Q.empty())) {

        int num = Q.size(); // Get number of strings to inspect at level
        while (num-- > 0) {
            string s = Q.front();
            //cout << "pop  " <<s << endl;
            Q.erase(Q.begin());
            V.insert(s);
            if (s == end) return level;
            for (int i = 0; i < s.size(); i++) {
                char c = s[i];
                for (auto l: letters) {
                    s[i] = l;
                    if ((V.find(s) == V.end()) && (B.find(s) != B.end())) {
                        //cout << "push " << s << endl;
                        Q.push_back(s);
                    }
                    s[i] = c;
                }
            }
        }

        // increment level after we have exhausted strings at previous level
        level++;
    }

    return -1;
}
};

min-in-rot-sorted-arr

Suppose an array sorted in ascending order is rotated at some pivot unknown to you beforehand.

1
(i.e.,  [0,1,2,4,5,6,7] might become  [4,5,6,7,0,1,2]).

Find the minimum element.

You may assume no duplicate exists in the array.

1
2
3
4
5
6
7
8
9
Example 1:

Input: [3,4,5,1,2] 
Output: 1

Example 2:

Input: [4,5,6,7,0,1,2]
Output: 0

Notes

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
- no dups
- rotation pivot in not known?
- sorted in ascending order
    - min should be at pivot
- peak just before pivot if pivot is not 0

1, 3, 5 --> pivot is at 0 - min is 1
56781234 --> min is 1 
min 
5

test 6
test 7
test 8
test 1 ---> min is 1
break

The following is a O(n) solution

1
2
3
4
5
6
7
8
9
10
11
int findMin(vector<int>& nums) {
    int min = nums[0];
    for (int i = 0; i < nums.size(); i++) {
        if ((i < nums.size() - 1) &&
            nums[i] > nums[i+1]) {
                min = nums[i+1];
                break;
            }  
    }
    return min;        
}

There is a O(logn) solution that uses binary search!

word-search

Given a 2D board and a word, find if the word exists in the grid.

The word can be constructed from letters of sequentially adjacent cell, where “adjacent” cells are those horizontally or vertically neighboring. The same letter cell may not be used more than once.

1
2
3
4
5
6
7
8
9
10
11
12
Example:

board =
[
  ['A','B','C','E'],
  ['S','F','C','S'],
  ['A','D','E','E']
]

Given word = "ABCCED", return true.
Given word = "SEE", return true.
Given word = "ABCB", return false.

Notes

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
DFS would be te desired approach.

We can iterate the arrays and when we find the first matching letter we start testing the neighbors
and continue to do this until we find all of them...if it fails somewhere we backtrack and try next one

For 'SEE'

We find 'S' at board[2][0]

need functions for getting each neighbor

check top neighbor, it's 'A'
check left neigbor, none
check right neighbor, 'F'
check bottom neighbor, 'A'

not found so keep iterating

note we need to ensure that we mark visited nodes
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
bool dfs(vector<vector<char>>& board, string word, int i,  int j, int p) {
    if ((i < 0) || (j < 0) || (i >= board.size()) || (j >= board[0].size())) return false;
    
    if (p >= word.size()) return true;

    if (word[p] == board[i][j]) {
        char c = board[i][j];// for caching currently inspected char
        //cout << "checking " << c << endl;
        board[i][j] = 0;//erase temporarily to mark as visited
        // check top neighbor
        //cout << "check top\n";
        if (dfs(board, word, i - 1, j, p+1)) return true;
        // bottom
        //cout << "check bottom\n";
        if (dfs(board, word, i + 1, j, p+1)) return true;
        // left
        //cout << "check left\n";
        if (dfs(board, word, i, j - 1, p+1)) return true;
        //right
        //cout << "check right\n";
        if (dfs(board, word, i , j + 1 , p+1)) return true;

        // we need to restore char at end of each run
        board[i][j] = c;
    }

    return false;    
}

bool exist(vector<vector<char>>& board, string word) {
    for (int i = 0; i < board.size(); i++) {
        for (int j = 0; j < board[0].size(); j++) {
            if (dfs(board, word, i, j, 0)) return true;
        }
    }
    return false;
}

This works for most cases but here is an example where it fails 😧

1
2
board = [["a"]]
word = "a"

We need to consider the case of single letter words.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
bool dfs(vector<vector<char>>& board, string word, int i,  int j, int p) {
    if ((i < 0) || (j < 0) || (i >= board.size()) || (j >= board[0].size())) return false;
    
    if (p >= word.size()) return true;

    if (word[p] == board[i][j]) {
        char c = board[i][j];// for caching currently inspected char
        //cout << "checking " << c << endl;
        board[i][j] = 0;//erase temporarily to mark as visited
        // check top neighbor
        //cout << "check top\n";
        if (dfs(board, word, i - 1, j, p+1)) return true;
        // bottom
        //cout << "check bottom\n";
        if (dfs(board, word, i + 1, j, p+1)) return true;
        // left
        //cout << "check left\n";
        if (dfs(board, word, i, j - 1, p+1)) return true;
        //right
        //cout << "check right\n";
        if (dfs(board, word, i , j + 1 , p+1)) return true;

        if (word.size() == 1) return true;

        // we need to restore char at end of each run
        board[i][j] = c;
    }

    return false;    
}

bool exist(vector<vector<char>>& board, string word) {
    for (int i = 0; i < board.size(); i++) {
        for (int j = 0; j < board[0].size(); j++) {
            if (dfs(board, word, i, j, 0)) return true;
        }
    }
    return false;
}

max-prod-three-nums.md

Given an integer array, find three numbers whose product is maximum and output the maximum product.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
Example 1:

Input: [1,2,3]
Output: 6

Example 2:

Input: [1,2,3,4]
Output: 24


Note:

    The length of the given array will be in range [3,104] and all elements are in the range [-1000, 1000].
    Multiplication of any three numbers in the input won't exceed the range of 32-bit signed integer.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
3 * 2 = 3 + 3  OR 2 + 2 + 2

0 * num -> 0
1 * num -> num

big num * num2 * num3

num * -big num * -num

order of input not sorted

can we sort it?
yes

allows us to pick large positive numbers and small negative numbers

[-345, -23, 0, 0, 23, 245, 1000]


what about 2 numbers?
-345, -23 ?
245, 1000 ?

what if you have

[-345, -23, 0, 0, 1000] ?

[-345, 0, 0, , 1, 1000]


we need to avoid any zeroes?
but zero is larger than negative....so could be valid in some cases
ex: [-30, -20, 0 , 0, 4] - here 0 is biggest we can have? no... -30*-20*4 is

[1, 2, 100, 1000, 100000] --> in this case we only need to look at the end of array
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
int maximumProduct(vector<int>& nums) {
    if (nums.size() == 3) return (nums[0]*nums[1]*nums[2]);

    // sort the vector in asc order
    std::sort(nums.begin(), nums.end());
    int res = 0;
    int last = nums.size() - 1;
    // if first two elements negative then we need to check the product
    if ((nums[0] < 0) && (nums[1] < 0)) {
        int next_index;

        if ((nums[0]*nums[1]) > (nums[last] * nums[last - 1])) {
            res = nums[0]*nums[1];
            next_index = last;
        } else {
            res = nums[last] * nums[last - 1];
            next_index = last - 2;
        }
        res *= nums[next_index];
    } else {
        res = (nums[last] * nums[last - 1] * nums[last - 2]);
    }
    return res;
}

This solution is longer than it needs to be (and also seems to fail for some corner test cases).

A simpler approach is as follows:

1
2
3
4
5
6
7
8
9
10
if (nums.size() == 3) return (nums[0]*nums[1]*nums[2]);
// sort the vector in asc order
std::sort(nums.begin(), nums.end());
int res = 0;
int last = nums.size() - 1;

int prod1 = nums[0]*nums[1]*nums[last];
int prod2 = nums[last]*nums[last-1]*nums[last -2];

return max(prod1, prod2);

This is a nlog(n) approach.
It is possible to do this in O(n).