Problem described here.

Breakdown

• We have an inter

Background

An algorithm is greedy if it tries to find the best local solution at each step with the hope that the best global solution will be found in the process. And sometimes this works!

Schedule as many seminars as possible

Let’s say you were at Comic-con and wanted to ensure that you’re day was as full as possible. After all, you want to maximize your experience.

And these are your options:

This looks something like this:

We need to look at a few more examples to come up with a strategy of picking the right seminars. Let’s have a look at a few generic examples of events below.

But let’s look closer at why we pick these and how we would formalize it.

Breakdown

If we just picked the shortest events, that may not always be optimal. Picking the ones that start the earliest is
also not enough.

Steps

1. Pick the seminar with the earliest end-time
2. Now you pick a seminar that starts right after this one. If you get more than one, then pick the one that ends soonest.

A good example is the Task Scheduler.

Problem

Breaking it down

So the input is a string like this:

1

"245300"

And we need to delete 2 digits so that we get a minimum value.

Well, my first thought was something like this:

1
2
3
4
5

del 2 & 4 --> 5300
or del 2 & 5 --> 4300
or del 2 & 3 --> 4500
...etc...
or del 0 and 0 --> 2453

But boy does that get tedious fast 😧. Not to mention, that you basically have O(n^2) time which is not acceptable.
Ok so let’s first try some examples to understand the basic characteristics of a number.

Try visualizing

Let’s look at how a base 10 number is composed:

1

352 = 3 * 100 + 5 * 10 + 2

Which means that intuitively, each digit gets more weight as we move left. Each move left is an order of magnitude.
Armed with this understanding we can try to visualize the number as follows:

If we need to remove one digit and get the smallest value, can you see which one we would remove?

Note

1
2
3

Due to the nature of the problem, if we were to remove the digit `5`, we would end up 
with `30 + 2` and not `300 + 2`. Because we just 'slide' the the left number into the 
right's position to create a smaller number.

Let’s see another example. What if the input was 1432219 and we want to remove two digits?

Ok, let’s think of a sub-problem: what if we want to remove one digit?

1
2
3
4
5

432219
132219
143219
143229
143221

Well the smallest one there is 132219

Let’s look at this closer. Look at just the first two digits of that. What’s the smallest one? 13?
Interesting!

So that tells us that the first two digits really determine the result here.

But why?

Recall the diagram of the number we saw earlier? The left-most digit has the most weight and digits slide
left to right when a removal is performed. So, having understood that, we see that removing anything to the right of 4 will not take enough weight off. And removing 4 will remove the most weight since the 1 will slide into its place.

Solution A

Based on the idea above, we can solve the problem as a series of subproblems: remove one digit at a time until k digits
are removed. For each subproblem, we need to find a ‘peak’ and then remove that number.

JS

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30

/**
 * @param {string} num
 * @param {number} k
 * @return {string}
 */
var removeKdigits = function(num, k) {
    let res = []
    
    for (let i = 0; i < num.length; i++) {
        while (k > 0 && res.length > 0 && num[i] < res[res.length - 1]) {
            res.pop()
            k--
        }
        res.push(num[i])
    }
    
    // edge cases when we find no peak
    for (let i = 0; i < k; i++) {
        res.pop()
    }
    
    //remove leading zeroes
    let i = 0
    for (; i < res.length; i++) {
        if (res[i] === '0') continue
        else break
    }
    res.splice(0,i)
    return res.join('')||'0'
};

Note that we need to explicitly do pop() if we never found any peaks, such as in 33333 or 1234!
In this case, we should just delete k digits from the end (and not the beginning , recall that 65432 has a peak).

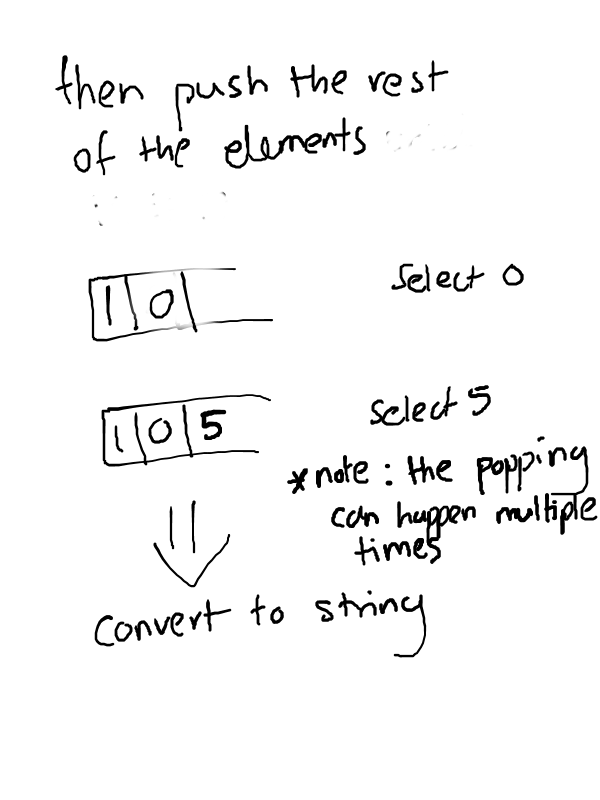
Also we need to strip out any leading zeroes. And for the case when we have all zeroes, such as 0000, we should explicitly return a 0!

Another thing to note is that in order to strip out leading zeroes we could have done String(Number(res.join(''))).
However, when the string is very long Number() could result in Infinity. So we do it manually instead.

This works, but the problem is that we are iterating the array for each sub-problem. So our runtime is O(k*n). We can
do better.

Solution B

Is it possible to somehow track the digits we have already visited?

Yes! We can use a list.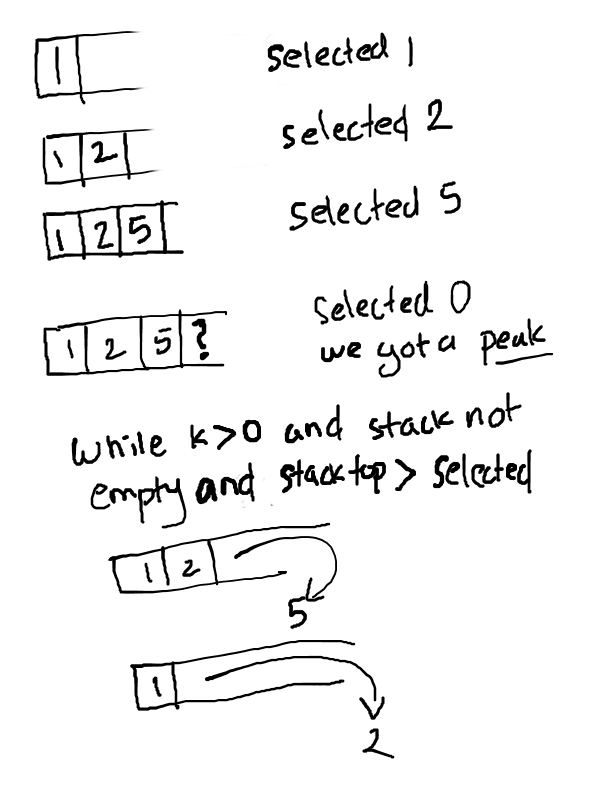

C++

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31

class Solution {
public:
    string removeKdigits(string num, int k) {
        string res;
        for (int i = 0; i < num.size(); i++) {
            while (k && 
                (res.size() > 0) &&
                (res.back() > num[i])
               ) {
                
                res.pop_back();
                k--;
            }                
            res.push_back(num[i]);
        }
            
        // handle case of never hitting a peak or not hitting
        // enough peaks
        for (int i = 0; i < k; i++) {
            res.pop_back();    
        }

        // skip leading zeroes
        int j = 0;
        for (; j < res.size(); j++) {
            if (res[j] != '0') break;
        }
        
        return (j == res.size()?"0":res.substr(j));
    }
};

The reason why we cannot do something like the following is that modifying the string while iterating it
is incorrect:

1
2
3
4

for (auto iter = res.begin(); iter != res.end(); iter++) {
            if (*iter == '0') res.erase(iter);
            else break;
        }

Obligatory hello world post.

Stay tuned for more!